For a final post this week, I'd like to make you wonder what it is like to slam your head bolt on in an accident while cycling. The agenda is objectively put some numbers out there and give a feel for things, using myself as an example. I'll show you how you can do the rough math yourself without much paper and ink.
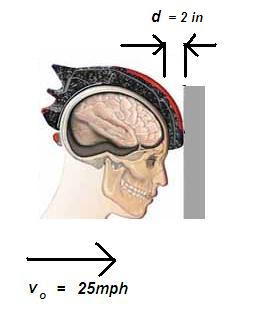
So I went over to the shelf and grabbed my utilitarian Giro bike helmet to see what the foam thickness on it would be. It came out to about 1.8 inches, so let's take it as 2 inches for sake of simplicity.
Now say one morning, I'm out riding my bike at 25mph on my street. Suddenly, out comes this mad old lady from hell, backing out of her driveway in her car without spotting me over her shoulder. Unable to react quickly, (yeah I had a hangover from last night) I can't swerve away in time and CRASH I do right onto the vehicle, with my helmeted head slamming onto glistening sheet metal.
My head just decelerated from 25mph to 0mph in seconds. What was my head's deceleration? Let's assume it is constant deceleration for an ideal condition. The best helmets should offer this condition.
Avoiding lengthy kinematics derivations, remember this equation for constant deceleration :

where
a = deceleration of the head with a negative sign
vo = initial speed = 25mph ~ 36.7 ft/s
d = distance the head moves after impact before coming to rest, which is the distance the foam crushed = 2 inches = 0.167 ft
Plug in the values and you get a = -4032.6 ft/sec^2 ------------> A
The acceleration due to gravity on the earth's surface is 32.2 ft/sec^2 -----------> B
Dividing A by B, my head just experienced a constant deceleration of 125 times that of gravity (125 g). That is after wearing a helmet!
If you look at the equation for deceleration above closely, the 2d term is in the denominator. Hence, the bigger thickness of foam you have, the lesser the deceleration becomes. If I had 2 times the foam as I originally had, my head's deceleration would be close to halved and I would have more distance to 'take' this deceleration over. But too much foam thickness doesn't yield a good helmet design as it can cause a host of other problems. So there's a trade off. You will also appreciate the fact that since the velocity term is in the numerator, the faster I go, the more g's of deceleration I experience.
So what about the force my head experiences during this impact? Well, here's another simple equation for you to remember, derived from the work and change in kinetic energy relationship :
where
m = mass of my head and F is negative in sign indicating a retarding force
Say my head weighs about 10 pounds or 4.5 kgs. Now (vo^2/2d) is simply acceleration we found above, which is 125g. Multiply that with 'm' = 10lbs and you get something in the order of 1250 lbs of retarding force smack against my head. To put that into perspective, that's half a metric ton hitting me right where I don't want it. What makes this so uncomfortable for me, even just to realize, is that its doing this to me in a fraction of a second. That fraction of a second yank on my head is a yank on my brain and its internal blood vessels.
The thing to realize is that 125g of force maybe enough to cause brain injury, leave alone anything higher than this. Rarely is constant force ever experienced in a real collision. A more realistic model would perhaps be force following a curve, reaching a peak when the foam is close to being fully crushed. Hence, the ideal helmet assumed here is sort of...well, ideal. As comments have told me, I acknowledge that this is a simplistic model that does not take rotational characteristics of the acceleration into account. Rarely does an impact between the helmet and the road go through the center of gravity, hence causing rotation of the head.
Another thing you will appreciate is that if I were without a helmet, there would be no soft landings at all. If epidemiological evidence suggests that, on averge, chances of serious brain injury are reduced by a factor of 5 by wearing a helmet, I get a big zero by not wearing one. Lost out there, didn't I?
Having said all this, I sincerely believe that in the coming years as we push the frontier into new materials, we will come up with better solutions for this energy management problem in helmets. We will realize the goal for softer landings, constant decelerations and peak forces of lesser magnitude. Until then, we are struck with what's out there in the market. Some of these helmets are improperly designed. On one hand, too stiff foam liners are used that break catastrophically on impact instead of crushing. On the other, to satisfy the goals of lightweight designs, there is also a tendency to select low density foams that absorb much lesser energy than what is required. Hopefully, these issues wil be addressed soon to give sportspeople the protection they need to keep their heads right.
ADDITIONAL READING :
How Bicycle Helmets Are Made (Video)
Engineering Aspects Of Human Skull Fracture (University of Tokyo, Japan)
* * *
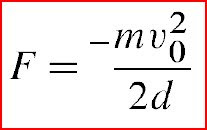




There is another impact to consider and this one is much more important. The impact of your brain on the wall of your skull.
ReplyDeleteIn accidents involving the human body there are always more than one impact to consider. The first is, of course, your body coming into contact with said immoveable object. The second is your organs smacking up against your body cavities. This impact is what will inevitably cause you the most distress.
It would be interesting also, for instance, to look at how the impact that your brain encounters differs when you consider things like age and hydration. Afterall, your brain has a kind of helmet already. It even has a cushy fluid surrounding it besides the actual skull. This fluid and the space it takes up will help dictate how well your brain fairs in the impact with the inside of your skull.
This fluid may be affected by things like how hydrated you are. The more dehydrated you are the less fluid there is surrounding your brain? Then how does this afftect the all-important brain/skull collision?
Take also into consideration the age of your brain. As you get older your brain shrinks. This, in turn, increases the distance from your brain to your skull. How does this affect the impact and the subsequent forces?
Does any of this change anything to any meningful amount?
Flatmtber : I'm not sure what the thickness of the skull on average is, for both men and women. But I did a small Google search and learned that researchers at Ford Motor Company and Tianjin University of Science and Technology studied 3,000 people for skull thickness and shape. They found that skull thickness was on average 6.5 millimeters in men and 7.1 millimeters in women. Men have lesser skulls than women? Huh? Interesting!
ReplyDeleteYou may be right also about age affected how well the brain is seated in the skull.
How skull thickness, skull shape and the brain interacts on head impact is probably something of research and is out of the scope of this blog at the moment. Nevertheless, what I've shown gives one a pretty good picture of what we're talking about.
Nice article with basic physics. I'd be tempted to do it on a "time-based" interval for deceleration of the noggin, since it's unlikely that the foam will be flattened to a null thickness - and that compression of the foam might make the relationship non-linear.
ReplyDeleteI'll look a bit into this. I really enjoy these posts in your blog, Ron!
Rod,
ReplyDeleteYes this was sort of a dumbed down approach, where in reality impact energy sustained by the head is of non-linear nature. Almost everything in this world is non-linear but much time and effort can be spent understanding it whereas my intention was to just give a quick, rough picture of what happens on impact.
Like flatmtber above said, it would be very interesting to know from medical science, what forces and accelerations the brain can take before blood vessels are torn and neurons stretches beyong the point of repair, and also how different skulls, and thicknesses interact with EPS foam of given dimensions.
You also say that is unlikely the foam can be flattened to null thickness. But I think it is also likely that a helmet was manufactured with too thin or "soft" a lining such that the foam 'bottomed out' well before it could slow the head to a stop. These things do happen. It makes me uncomfortable to know it does, and that these things are beyond our control and rests more with the company responsible for the helmet.
Considering the huge forces involved in a full-on crash, I think it's a good thing that very often the shell of the helmet will skid instead of just absorbing the impact full-on. I remember reading something on Velonews about helmet manufacturing and testing. I'll try to find that old issue.
ReplyDeleteThanks again, I like that you make physics applicable and simple to understand :)
The car is actually likely to yield far more that the foam of the helmet. I have never seen the foam of a helmet actually squashed significantly and certainly not flat and I very much doubt that the elastic region of the deformation (which wouldnt be obvious after the event)is significant, wheras I have put my head into the odd car panel and left a very noticable dent that probably accounts for a good couple of inches of travel.
ReplyDeleteAs a matter of interest, the limit for concussions is generally taken to be around 80G, though studies of football players suggest that 100G is more common but concussions can still occur below this level. The Snell standard (which most helmets DONT pass), requires a deceleration of less than THREE HUNDRED G!!! (but that uses a genuinely very solid head and "kerb" so the helmet really is the only protection.
This is a pretty decent 0th order analysis for an entry level examination but it really doesn't capture the physics at all.
ReplyDeleteto really go through what happens during an impact you need to take a look at the detailed wave dynamics going on between headform, foam layer and impactor and bring in stuff like equations of state, hugoniots loading paths, etc
you can then more or less directly get a feel for induced particle velocities, accelerations, etc.
another thing to consider, as someone suggested, is that foam loading is highly non-linear. As foam is impacted it compresses - as it reaches dense packing the utility of the foam quickly diminishes.
with all that in mind, hellmets have a more or less definitive upper impulse threshold after which they really don't do squat.
this is also ignoring all of the stuff that goes on with the brain - torsion, getting bounced around, etc)
I think the lesson learned is you should be riding slower in your neighborhood! 25mph is my sprint!
ReplyDeleteAnyway, in the helmets that I have seen after a crash it seems very common for them to be cracked not crushed, I would want to see how the forces of it splitting apart absorb the energy from impact vs the compression.
Jason : Thank you for the comments. An nth order simulation is out of the scope of this blog. Hopefully, as my understanding improves, I may write about it, as it is a topic that interests me.
ReplyDeletePhilip : They make those foams too stiff, that's the problem. They do so because in the helmet drop tests, they use a solid headform and so have to design the foam in such a way that the headform does not crush the foam. However, that's not an accurate simulation of the human head which can deform elastically. Its not as solid as a headform. I've always wondered why they can't use something akin to ballistics gel or something that mimics the human head more than a headform made like a lead ball.
Ron, I'd recommend you get a hold of Drumheller's book: Introduction to wave propagation in nonlinear fluids and solids ISBN 0521587468, 9780521587464
ReplyDeleteHelmet cracking and apparent stiffness doesn't really reveal the degree of protection offered by the foam - what you are interested in is what sort of stress waves are being transmitted on the timescale of the impact event and how the foam modulates that, which is quite apart from observed damage.
You can look at it somewhat from two schools of thought. It can be seen purely as an impedance based attenuation of mechanical waves (and here the mechanics of material deformation are of limited relevance), or it can be seen as a mechanical attenuation of the stress waves by flattening out the transmitted stresses due to crushing until densification is reached (here you start evoking concepts of energy absorption as well).
I remain unconvinced which school of thought is correct (they yield incompatible results in some cases). My experience is more with shockwaves and in that case the shock impedance approach appears to be more valid (indeed in shock loading you can show that a very limited quantity of energy is absorbed on the timescale of the event) but I am unsure how that translates to the general wave dynamics case - and the concept of stress attenuation via straining seems intuitively accurate.
I'm ultimately not all that confident about bike helmets for serious cyclists (the 30 km/h+ crowd) - I suppose the saving grace is really that barring full on head first crashes into walls and tall vehicles the true impact on the head/helmet is neither planar nor is it close in terms of velocity to how fast one was actually travelling.
Thank you Jason. I'll keep the book you mentioned in mind. By the way, do you have any idea where one could obtain FEA of foam deformation for impacted bike helmets?
ReplyDeleteRon, your comment about using ballistics gel to simulate the head may not be practical as high vibrations in it might make the mean accelerations difficult to compute in a test simulation. Thanks.
ReplyDelete@ Gsport 6:37pm : The maximum tolerable deceleration of the human head is 300g, provided it is applied for just milliseconds on the time scale. This is what I read.
ReplyDeleteThe point is that as long as the way helmets are tested is stupid (solid steel headform) and the manufacturers are designing to pass the standards rather than to be good helmets, we will have helmets that are not a good match to our needs. In this day and age it should be a doddle to construct a more realistic head with stress gauges implanted, and make serious measurements of protection levels.
ReplyDelete@Ron
ReplyDeleteMost FEA codes that specialize in dynamic modelling employ some sort of proprietary "crushable foam model" that is variously based on engineering literature for constitutive relations, EOS, etc.
There is a lot of lit out there - you are probably well served using google scholar and searching stuff like
"Foam Crush Model"
The FEA manuals often source the lit they used as they often work with the researchers in question too.
I found this paper especially helpful though:
http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6V3K-3WRC6B1-5&_user=458507&_rdoc=1&_fmt=&_orig=search&_sort=d&_docanchor=&view=c&_searchStrId=941550657&_rerunOrigin=scholar.google&_acct=C000022002&_version=1&_urlVersion=0&_userid=458507&md5=bc66aba5999f054af6b0ee7b8096ca7b
@gsport,
the problem with your seemingly easy solution is that it is anything but easy. You need a material that closely matches the dynamic behavior of human tissues - said tissues are highly non-linear, visco-elastic materials.
Also you need to capture the detailed geometry and structure of the head
In short matching materials and structure to the real thing close enough so that you can measure stress-strain directly is very difficult.
Furthermore you've got another problem - injury thresholds and mechanisms are poorly understood, you've got a complex interplay between the medical people and the engineers trying to work out "engineering" values for medical phenomena without being able to do direct analysis on the real, live system.
Much of the data about thresholds is forensic and highly empirical based on "feel".
There is a reason they talk in terms of accelerations instead of stresses and strain rates - it is significantly easier to quantify the kinematics rather than the structural and wave dynamics.
It is more functional to create a headform that mimics the bulk dynamics (ie similar mass, neck compliance, etc for which there is more lit) and speak in terms of kinematics, than it is to go through from a detailed "mesoscale" stress/strain and wavedynamic analysis - the latter is naturally picking up steam especially as bulk concepts like energy conservation don't accurately predict behavior for anything but low speed impacts (ie low strain rates)
Vary unique blog.Bicycles math!
ReplyDeleteI really really like your blog,Ron. Its very different&interesting.Keep up the good work.
ReplyDeleteGab
Gabbie : Glad you're enjoying it.
ReplyDeleteAt Jason : The complexities are immense if you want to get really deep into this stuff. I presented a point mass discretized model here, and the level of abstraction is sufficient for any person not interested in too detailed analysis. Hopefully we can get back together again for detailed analyses. I've got to check out some literature before that first.
ReplyDeleteGsport said at 6:37pm : The car is actually likely to yield far more that the foam of the helmet. I have never seen the foam of a helmet actually squashed significantly and certainly not flat and I very much doubt that the elastic region of the deformation (which wouldnt be obvious after the event)is significant, wheras I have put my head into the odd car panel and left a very noticable dent that probably accounts for a good couple of inches of travel.
ReplyDeleteYou're right about the denting. Check out this video I found of a racing cyclist rear ending into a parked car by the side of the road. I did not expect the car to deform as much as the video shows.
Jason,
ReplyDeleteYou are right, EXACTLY modelling a human head is always going to be very difficult. However, to throw up our hands and use a steel headform with a single accelerometer seems like a poor second best.
It wouldnt be THAT difficult to create a fibreglass "skull" (of a suitable stiffness) with strain gauges AND accelerometers, covered in a "gel" and do tests to compare it to how a REAL human head (from a donated body) perform under the tests. We would then have valuable data about how the artificial test-skull compares to a real one, and subsequent tests on "test-skulls" whilst not by any means, perfect, would be substantially more accurate than existing tests on steel heads that are virtually unyielding.
Helmet design might then advance to try to match the performance of the helmet to the behaviour of the skull and address some of the issues with existing helmets on real heads...
There's a reason those mythbusters use ballistics gel to simulate human heads when blowing them up.
ReplyDelete@ gsport,
ReplyDeleteIt is actually very difficult to get cadavers for destructive testing in engineering.
Creating a headform of similar stiffness and structure is not enough - what is dramatically more important is replicating the hugoniots, impedances.
You could very well do all that (at significant cost to the consumer or taxpayer - we're trying to get people to wear the things remember?), however you then have to ask yourself what you are going to gain from it all. The major impediment to helmet performance is not the testing apparatus but what a cyclist is willing to wear due to comfort and aesthetics.
Design constraints are the real problem, not the diagnostics.
@Ron
Mythbusters doesn't do real science though, most of the research and R&D in blast loading is conducted with relatively standard crash test dummies with accelerometers and surface mounted pressure transducers - in those cases you are interested more in what the body form sees through protection systems.
Jason said : Mythbusters doesn't do real science though, most of the research and R&D in blast loading is conducted with relatively standard crash test dummies with accelerometers and surface mounted pressure transducers - in those cases you are interested more in what the body form sees through protection systems.
ReplyDeleteI didn't say they're doing real science. Sometimes, approximations are needed by engineers and common people to test, prove, make a product etc. According to the Mythbuster guys (who themselves have worked in special effects for sometime), ballistics gel closely simulates the density and viscosity of human muscle tissue and is used for testing the performance of firearms ammunition. I was only asking whether something of this nature would be far better than using a rigid, metal headform. Throw some ideas around.
Jason. Look into "Stylene". I have read a few research papers that used this material to simulate human scalp. Sort of a rubber. I'm not sure if there's anything out that that can mimic human skull that is made of 22 bones. In bone grafting, they use some clever materials to mimic the porous structure of bone. Might this help?
ReplyDeleteBy the way, do you sincerely believe the drop anvil test on the metal head form done by helmet companies today is inadequate? What do you propose they do more?
Interesting discussion. May I also add the mythbuster's use pig cadavers. The ethical implications of using animal body parts are many. I still think if you want to save a human's life, its best to test on a human cadaver.
ReplyDeleteJason said:-
ReplyDelete"Creating a headform of similar stiffness and structure is not enough - what is dramatically more important is replicating the hugoniots, impedances.
You could very well do all that (at significant cost to the consumer or taxpayer - we're trying to get people to wear the things remember?), however you then have to ask yourself what you are going to gain from it all. The major impediment to helmet performance is not the testing apparatus but what a cyclist is willing to wear due to comfort and aesthetics.
Design constraints are the real problem, not the diagnostics.
There is a reason they talk in terms of accelerations instead of stresses and strain rates - it is significantly easier to quantify the kinematics rather than the structural and wave dynamics."
In my opinion, one of the biggest design constraints right now is that the helmet should cushion an unyielding steel headform, this means that the amount of helmet material involved in the collision is restricted to a very small volume over a pretty small contact patch. With a real skull, the skull would deform slightly (like a bike tyre) to create a larger contact patch with a larger volume of helmet material involved in the decceleration.
As a result (in my opinion) a better helmet would have a slightly softer foam that in the worst case scenario impact we would see almost fully flattened over a large area by the riders head. This would result in a more flexible possibly lighter helmet that would likely be more comfortable and easier to "fit" too, all of which is likely to improve adoption.
Sure there is a huge amount that is unknown about head injuries, the role of angular acceleration is the obvious one, however what IS known is that:-
1. The human head is not a rigid steel headform.
2. People dont wear helmets due to issues with fit, feel and comfort (not just how they look).
3. Helmet manufacturers design to pass the tests.
I would be much happier using a helmet that had proved it could deccelerate a flexible head (with a similar stiffness to a human skull) at 100G from 20mph (where the strain in a fibreglass headform made to be a similar stiffness to a human skull did not exceed 75% of "yield strain") and had "used up" all it's protection than:-
Using a helmet designed simply to prevent an unyielding steel headform decellerating at more than 300G from 6.3m/sec (14mph).
Using a similar calculation to Ron's initial one, you could pass the Snell test (which most helmets dont pass) with 7mm of cushioning (travel), wheras a 100G from 20mph test would need 40mm of travel, which might be made up of 5 or even 10mm of skull deflection and the compression of an inch and a half of helmet...
Wouldnt you?
In summary, my point is that we dont have to create a "perfect" test, just a "much better" one, and I honestly dont think that that is THAT hard.
Jason, Gsport : Do you have any comment on the use of honeycomb structure for helmets? One was shown recently on the Yanko Design blog and the design is being pursued by some French firm named DoYouVelo?
ReplyDeleteSee here for more details.
The honeycomb/folding design looks really neat, you can see comfort and ventilation being very good. However I think there is an inherant problem with using a member that will buckle, as I would think these ribs will. The stiffness will start at a maximum, tail off slightly as it begins to buckle, then drop almost to zero once buckling really starts. I suppose with this shape, as the first ribs to hit buckle, others will come into play as they make contact, so that may counteract it somewhat, however you are giving up any protection in the initial zone..
ReplyDeleteChances of selling a helmet that looks like that and ties on with a ribbon like a bonnet to serious cyclists in any discipline? Pretty much zero I would think...
Ron, the design brief said the objective was to create something for minor bumps and falls. The issue of buckling seems real, so my question is ...after a minor fall, is it elastic enough to come back into its original shape? Who knows. Its still not a bad idea, and it looks like it will really excel in the cooling of the head.
ReplyDeleteSorry for the late reply.
ReplyDelete@ Gsport:
I think you've got some valid points but you are missing a huge aspect of foam behavior - as foam compacts beyond a certain point it becomes useless.
Ron's treatment is entirely based on the concept of trading space for time - which is perfectly valid but it ignores the fact that once the foam reaches dense packing (all the voids are collapsed) its only providing impedance attenuation of the stress waves - of course if you are a driving a shock into the foam all its doing is impedance attenuation, but I think most crashes remain largely acoustic.
You're falling into a similar pitfall by assuming that a helmet that pancakes out to a dramatic degree would better protect the head. The reality is that if you look at the dynamic stress strain curves of a foam you'll observe they are largely elastomeric: there is a large range of strains for which the stress remains relatively constant after which it starts to rise precipitously (this corresponds with densification).
You want your foam to be operating as much as possible in that plateau region, otherwise you risk the stress being quite high and the foam doing nothing. Going to a softer foam might involve requiring a significantly greater thickness for impact protection.
I also think you are heavily over-estimating the compliance of the skull - its fairly rigid in comparison to both the foam and especially the brain.
@Ron:
I have issues with the anvil testing - for one it ignores the most important dynamics: the brain bouncing and torquing inside the skull, the second is that it ignores the rest of the neck and body attached. I think they could do much better with tissue simulants for a scalp and brain with a rigid headform (metal is probably fine) and an actual neck
again, I think its somewhat academic, since as I said before the limitation is comfort and ergonomics not really testing.
Jason I think you are making this far more complex than is necessary.
ReplyDelete1. I do not believe that existing helmets ever achieve a state where the foam is "fully" compressed. We arent talking about elastomer foams here but typically expanded polystyrene and the foam often breaks before it compresses even a fraction as much as it could.
2. Whilst the brain will undoubtedly rattle about inside the skill, which seems to be your main concern; the initial impact and decceleration will surely be the worst of these wouldnt you agree? Broadly, if the brain is damaged by the first impact then the helmet has failed, and if the brain survives the first impact/deceeleration then it will most likley survive any subsequent waves that are set up.
3. An examination of decceleration is quick and easy, and I would argue that it is an established means of gauging "suvivability" and is what is used in the design and testing of car impact protection systems.
4. Whilst the human skull will not flex much, it will flex a lot more than a steel headform. When we are dealing with two mating curves, a slight defelction of the skull will correspond to quite a large change in the local radius of curvature which will make quite a difference in the contact area, and therefore pressure and therefore stress in the material.
5. Arent we arguing the same point? vis that the existing tests and helmets could be improved?
1) Current foam helmets do not completely compress because that is an explicit design feature for reasons I have stated above - you do not want your foam approaching dense packing.
ReplyDelete2) That is patently incorrect. There is significant conflicting theories and research on the precise wounding mechanics. There is some good data showing it is the torsion on the brain, and not the first impact into the skull which is the biggest problem.
3) Car crash testing involves measuring accelerations on dummies in various locations (head, chest) that are dynamic analogs to the human body, as well as accelerations in the vehicle.
That is quite different from what is going on in helmet testing where the whole head is treated as a unified mass.
I said previously acceleration is a good tool because strain gauges and the like are tough to use directly in impact.
4) I think you are mistaken if you think elastic deformation of the skull will bring a significant drop in stress in the skull. Also the wounding is caused by different accelerations of the brain WRT to the skull, so you are more interested in the stress states in the brain AND and the stress states/wave dynamics in the skull-helmet system - they are somewhat separate.
5) We are, but you are arguing for stuff (like softer foams) which isn't supported by the lit ;)
A slightly softer foam to a specific point might be better but you're always going to be fighting that stress riser point with any crushable system.
1. My understanding is that even in collisions that did result in injury to the brain there was little compression of the foam. If that is correct then SURELY the foam is too stiff? I would personally rather have a helmet that "runs out" of cushion (just) before I get brain damage, than one which will still have travel left long after the acceleration on my head becomes critical.
ReplyDelete2. I understand that angular acceleration is often thought to be far more serious than direct impact, but arent we still looking at (broadly) a situation in which the initial angular acceleration is still the critical factor?
4. My point is that the deformation of the skull will effect how the helmet is loaded rather than the brain. In turn, a lower pressure on the helmet would necessitate a less stiff foam.
1) I think its very tough to quantify how much compression actually occurs - its not a quantity you can ascertain without a look at the microstructure post crash and EPS tends to crack after a point anyway - which is not necessarily a bad thing.
ReplyDelete2) Yes and no, the brain being a squishy thing behaves strangely when it whacks into a solid - the best analogy i can think of is a block of jello in slow motion. You can observe torsional movement as the thing bounces off a surface.
4) Skull stiffness is variable depending on the part of the skull but is several orders of magnitude greater than anything else involved in the system, also the degree of deformation that is needed to appreciably change the contact patch is pretty huge - remember the "pressure" is transmitted in terms of stress waves and thus the skull contact patch geometry has a different influence than say the geometry of the impactor (which is profound in that it generates very different stress concentrations).
The case might be different for a child, whose skull is significantly less stiff however.
n1 conversation.
ReplyDelete